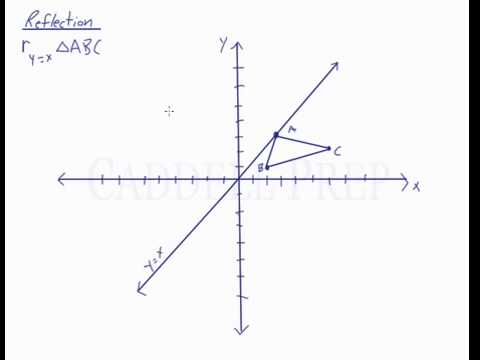
Related Pages Properties Of Reflection Transformation More Lessons On Geometry What is Reflection?If you change a function like f(x) to f(x), it flips the function over the yaxis!Reflections across the line y = x A reflection across the line y = x switches the x and ycoordinates of all the points in a figure such that (x, y) becomes (y, x) Triangle ABC is reflected across the line y = x to form triangle DEF Triangle ABC
Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor
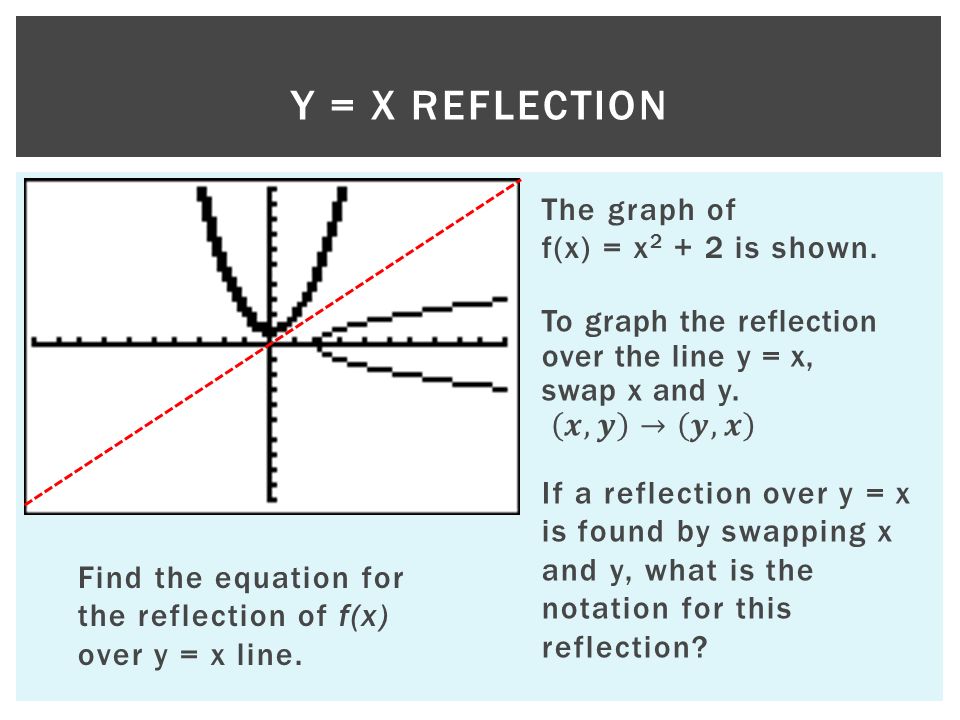
Equation for reflection over y=x
Equation for reflection over y=x-How Do You Graph a Reflection of a Function?Follow along with this tutorial to see how to take a function and reflect it over the yaxis



1
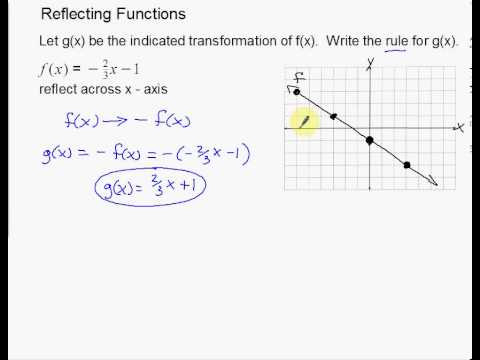
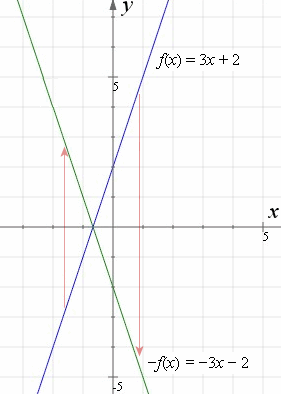
The equation of the line of the mirror line To describe a reflection on a grid, the equation of the mirror line is needed Example Reflect the shape in the line \(x = 1\) The line \(x = 1Summary Reflections and Rotations Reflections and Rotations We can also reflect the graph of a function over the xaxis (y = 0), the yaxis(x = 0), or the line y = x Making the output negative reflects the graph over the xaxis, or the line y = 0 Here are the graphs of y = f (x) and y = f (x)Reflecting functions examples We can reflect the graph of any function f about the xaxis by graphing y=f (x) and we can reflect it about the yaxis by graphing y=f (x) We can even reflect it about both axes by graphing y=f (x) See how this is applied to solve various problems This is the currently selected item
Reflections in Math Applet Interactive Reflections in Math Explorer Demonstration of how to reflect a point, line or triangle over the xaxis, yaxis, or any line x axis y axis y = x y = x Equation Point Segment Triangle Rectangle y =Transformation of Graphs Using Matrices Reflection A reflection is a transformation representing a flip of a figure Figures may be reflected in a point, a line, or a plane When reflecting a figure in a line or in a point, the image is congruent to the preimage 49/50 Satisfaction Rating over the last 100,000 sessions As of 4/ Reflection across the yaxis y = f ( − x ) y = f (x) y=f (−x) Besides translations, another kind of transformation of function is called reflection If a reflection is about the yaxis, then, the points on the right side of the yaxis gets to the right side of the yaxis, and vice versa
If point on a shape is reflected in the line y = −x both coordinates change sign (the coordinate becomes negative if it is positive and vice versa) the xcoordinate becomes the ycoordinate and the ycoordinate becomes the xcoordinateFollow along with this tutorial toFree linear equation calculator solve linear equations stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy



How To Reflect A Graph Through The X Axis Studypug



Reflection
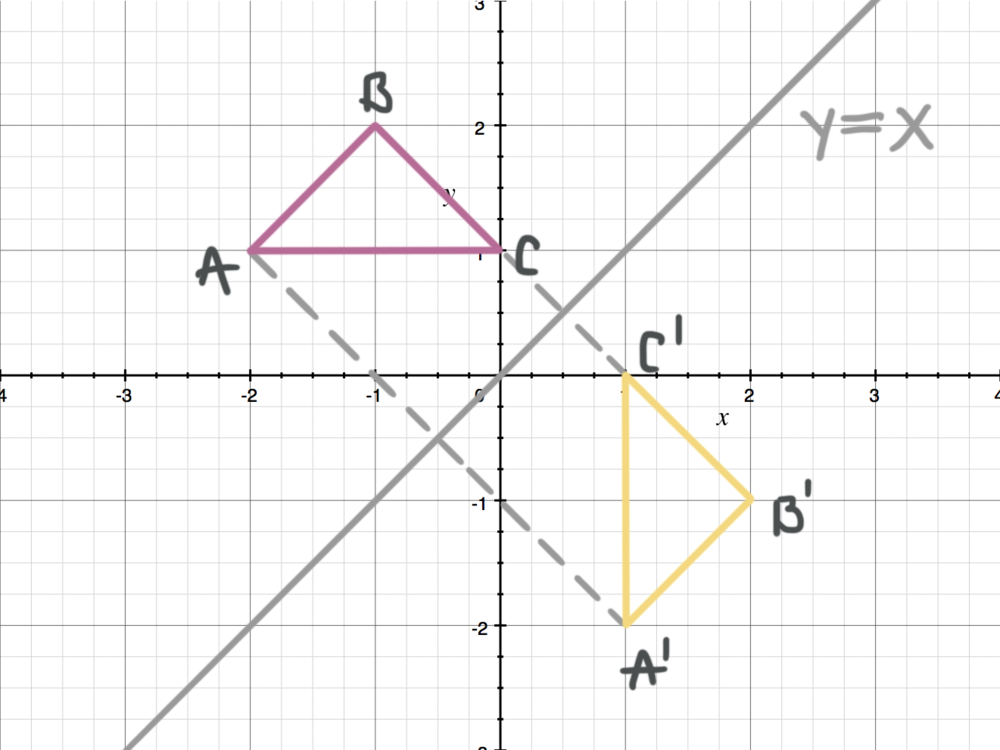
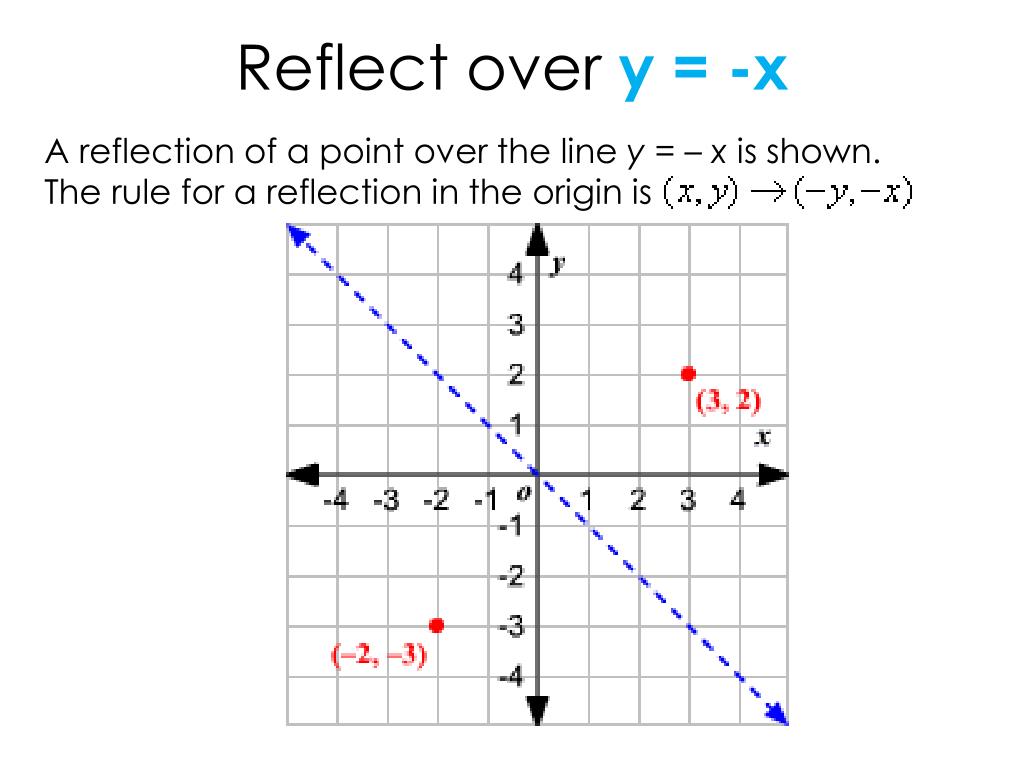
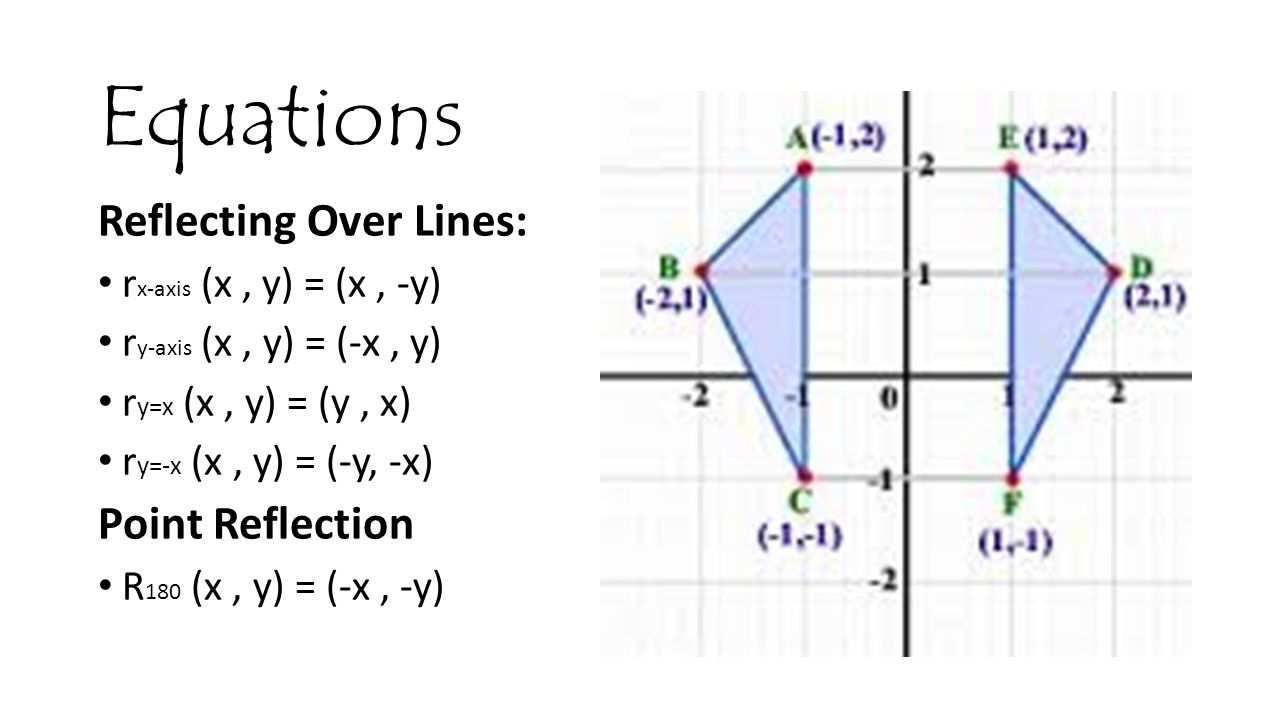
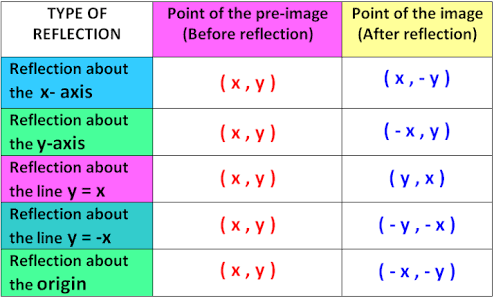
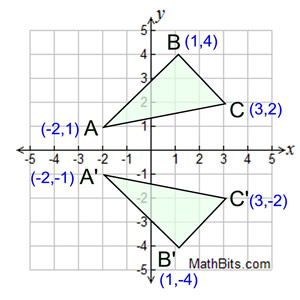
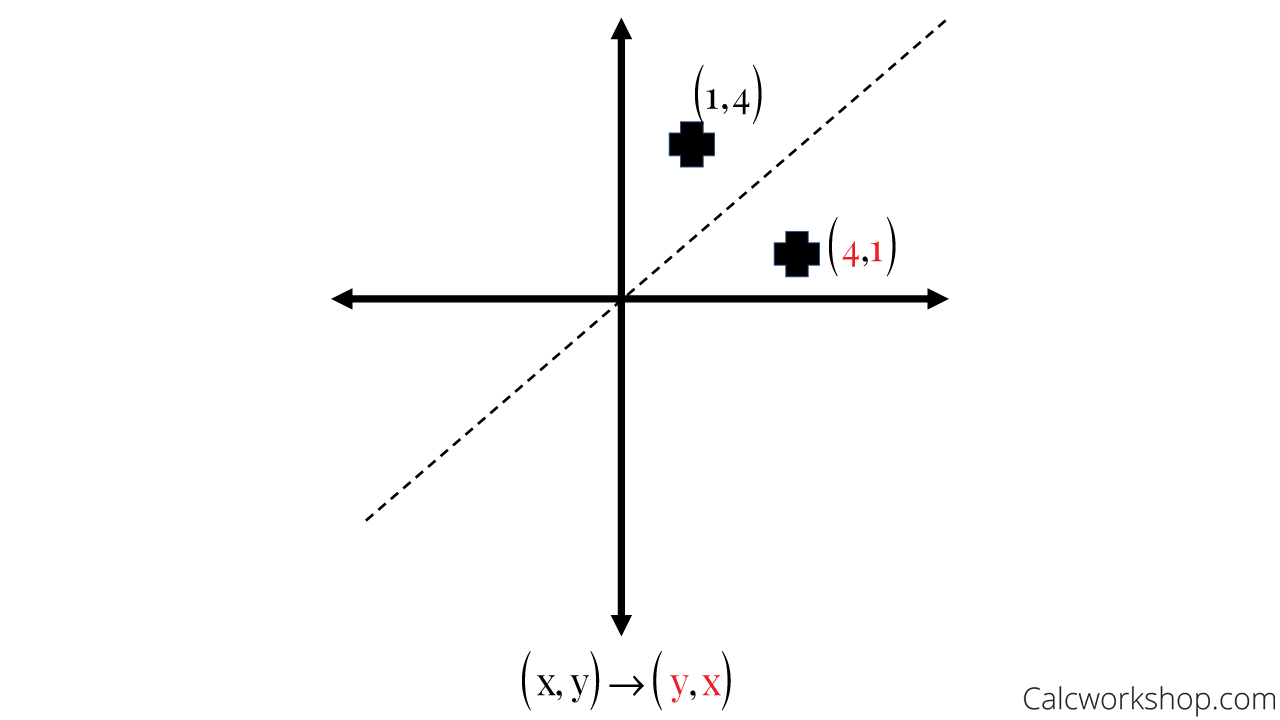
The fixed line is called the line of reflection A reflection of a point over the line y = − x y = −x is shown The rule for a reflection in the origin is (x, y) → (− y, − x) Explanation It's astonishing how difficult it is to find a good explanation how to reflect a point over aIn a reflection transformation, all the points of an object are reflected or flipped on a line called the axis of reflection or line of reflection Example A reflection is defined by the axis of symmetry or mirror lineIn the above diagram, the mirror line is x = 3Reflection over yaxis (x, y) (x, y) Reflection over xaxis (x, y) (x, y) Reflection over line y = x (x, y) (y, x)




How To Reflect Quadratic Equations Video Lesson Transcript Study Com
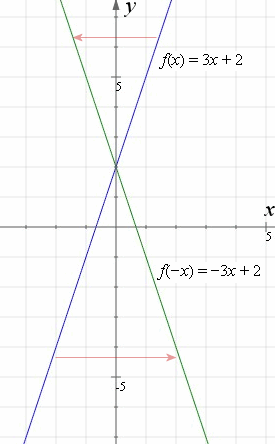



How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics
To reflect the absolute value function over the xaxis, we simply put a negative sign before the symbol (in this case the absolute value bars) Our new equation would be y = Ix3I Check the graphs in your calculator, they should look like a mirror image of each other, reflected over the xaxis Now try reflecting reciprocal y = 1/x 4Graphing Reflections In addition to shifting, compressing, and stretching a graph, we can also reflect it about the x axis or the y axis When we multiply the parent function f (x) = bx f ( x) = b x by –1, we get a reflection about the x axis When we multiply the input by –1, we get a reflection about the y axisFirst shift three units to the left, so the line of reflection becomes the y axis, then flip, and finally remember to shift three units back to the right to put the center line back where it belongs (This gives the f ( 6 − x) solution you already know) Replace x with 6 − x




Reflecting Functions Examples Video Khan Academy



How To Reflect A Graph Through The X Axis Studypug
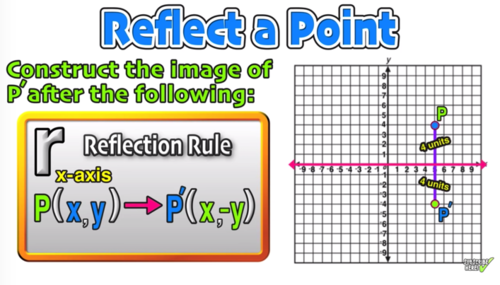
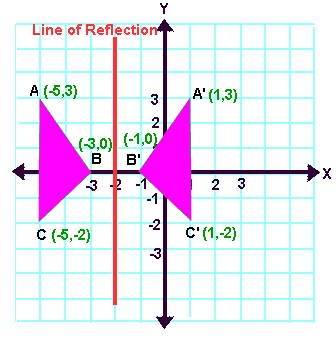
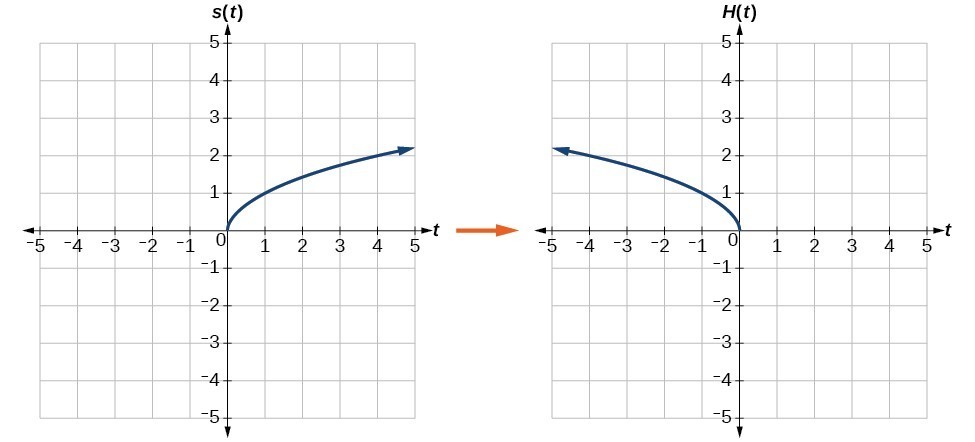
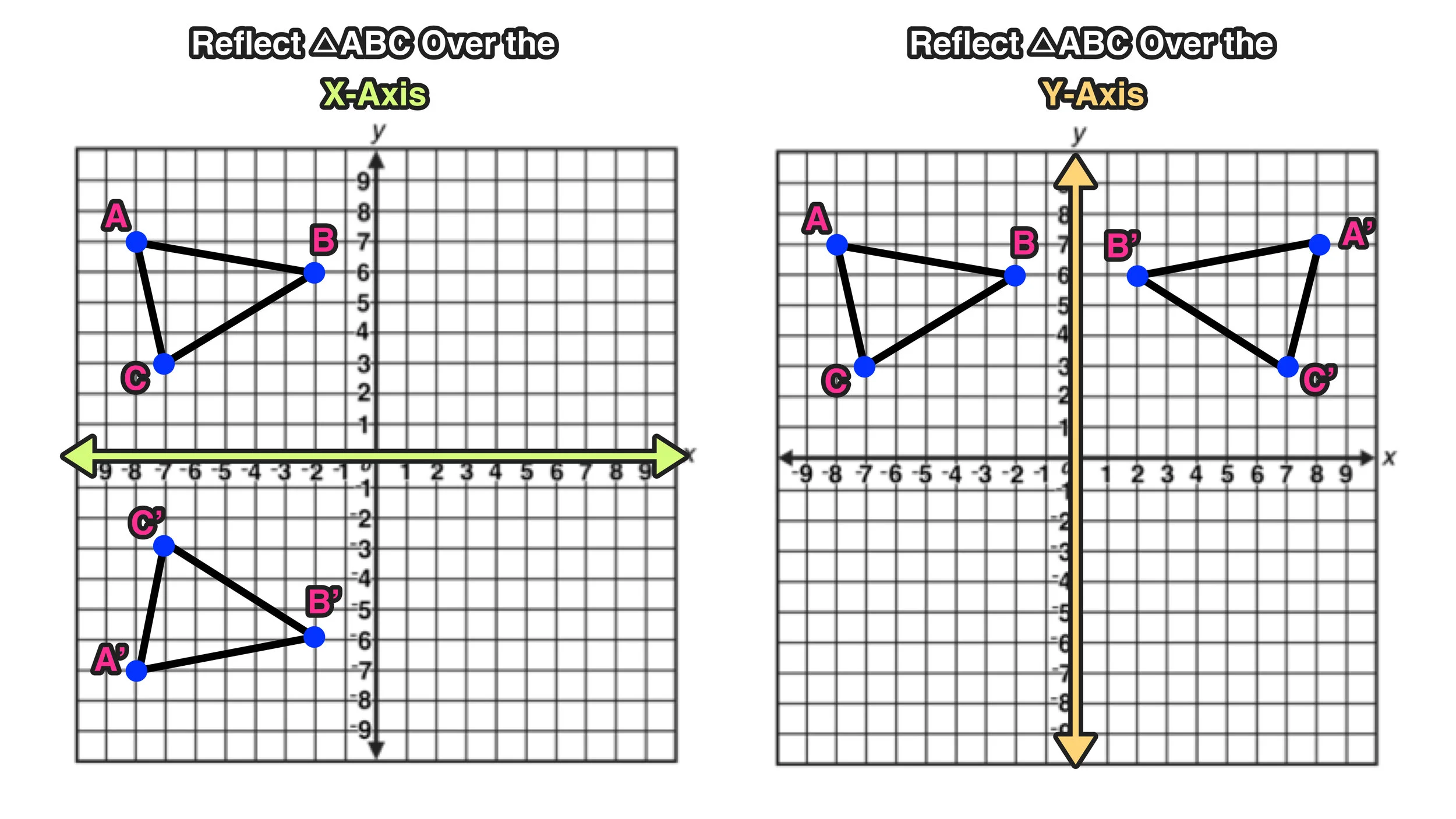
Reflect over the yaxis When you reflect a point across the yaxis, the ycoordinate remains the same, but the xcoordinate is transformed into its opposite (its sign is changed) Notice that B is 5 horizontal units to the right of the y axis , and B' is 5 horizontal units to the left of the y axisThis tutorial shows you how to reflect a function over a chosen line! The rule for reflecting over the X axis is to negate the value of the ycoordinate of each point, but leave the xvalue the same For example, when point P with coordinates (5,4) is reflecting across the X axis and mapped onto point P', the coordinates of P' are (5,4)
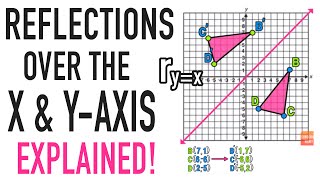



Reflections Over The X Axis And Y Axis Explained Youtube



Reflection Over The X And Y Axis The Complete Guide Mashup Math
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators1 y = x^2 is an example of a Quartic polynomial Constant function Linear function Quadratic equation 2 If we reflect y = x^22 over the xaxis we would get y = (x)^2)2 y = (x)^2)2Given a function f ( x) \displaystyle f\left (x\right) f (x), a new function g ( x) = f ( − x) \displaystyle g\left (x\right)=f\left (x\right) g(x) = f (−x) is a horizontal reflection of the function f ( x) \displaystyle f\left (x\right) f (x), sometimes called a reflection about the y axis



Linear Reflections Across X And Y Axis Example Youtube



Transformations Boundless Algebra
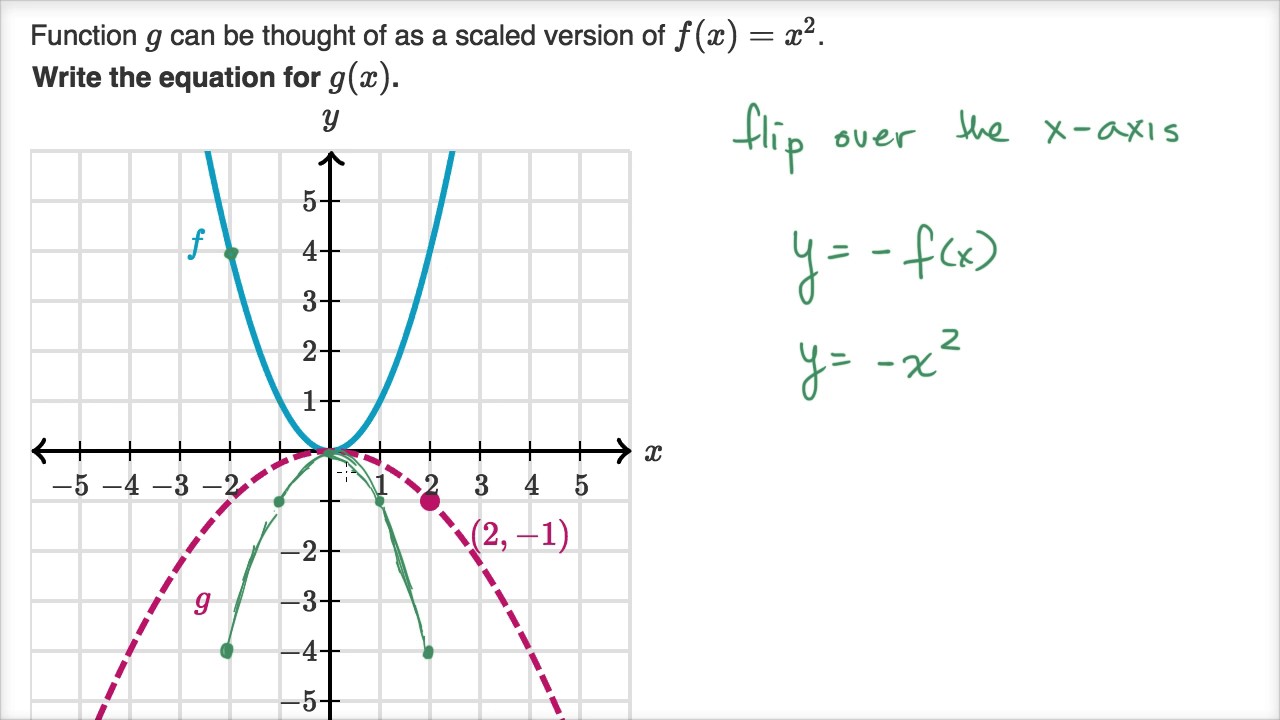
The graph of y=k⋅x² is the graph of y=x² scaled by a factor of k If kGet the free "Reflection Calculator MyALevelMathsTutor" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Education widgets in WolframAlpha👉 Learn how to reflect points and a figure over a line of symmetry Sometimes the line of symmetry will be a random line or it can be represented by the x



Ppt Reflect Over Y X Powerpoint Presentation Free Download Id




Common Reflections Key Stage 3
A small modification to your method will do the trick To reflect a point in a line, you need to reverse its orthogonal rejection from the lineOdd Function A function f f is called an odd function if f(x)= −f(−x) f ( x) = − f ( − x) for all x x in the domain of f f In other words, a function is odd if performing a reflection about the y y axis and x x axis (doesn't matter which is performed first) does not change the graph of the function To help remember the definition If I put f(x) = x^2 that would just reflect it over y=0 so the origin And adding two to x^2 2 would just raise it up to the reflect line which is asked for Isn't that the same for a equation like e^x or any other form of f(x) Reply #6 Mentallic Homework Helper



Rotation Rules



Reflection Transformation
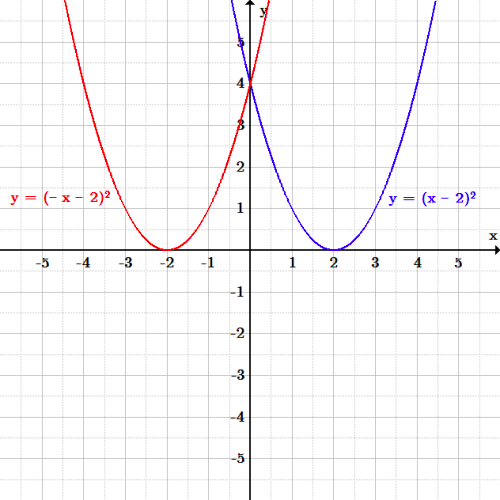
The reflection of such a parabola over the xaxis is simply written as y = (x^2) In other words, the function of f ( x ) becomes f ( x ) when reflected over the x axisApply a reflection over the line x=3 Since the line of reflection is no longer the xaxis or the yaxis, we cannot simply negate the x or yvalues This is a different form of the transformation Let's work with point A first Since it will be a horizontal reflection, where the reflection is over x=3, we first need to determine the distance of the xvalue of point A to the line of reflectionQ) and (r, s) (In the graph below, the equation of the line of reflection is y = 2/3x 4 Note that both segments have slopes = 3/2, and the shorter segments on both sides of the line of reflection also have slopes = 3/2 If you are using a xy coordinate axes drawn with a 11 aspect ratio, you can find preimage and image points by just counting



Transformations In Carnivals Ppt Video Online Download



1 5 Shifting Reflecting And Stretching Graphs
How Do You Graph a Reflection of a Function?Remember that when a point P (x, y) of the coordinate plane is reflected in the y axis , it becomes the point Q (x, y) and when reflected in x axis, it becomes P' (x, y) Therefore the quadratic p (x) = ax^2 bx c (a not zero) when reflected in y axis it becomes ;Answer (1 of 3) This is a method used to find the reflection over the line y = x, aka finding the multiplicative inverse of elementary functions for a function y of x, switch your x and y variables solve for y That gives us the reflection For example, if we had y = 3x 6, switch x and y



Reflection Over The Line Y X Youtube
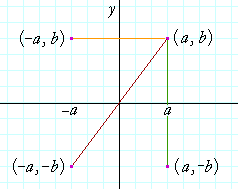



Reflections Of A Graph Topics In Precalculus
When you reflect a point across the yaxis, the ycoordinate remains the same, but the xcoordinate is transformed into its opposite When working with the graph of y = f (x), replace x with x Reflection in y = x When you reflect a point across the line y = x, the xcoordinate and the ycoordinate change places Reflection across the yaxis y = f ( − x ) y = f (x) y=f (−x) Besides translations, another kind of transformation of function is called reflection If a reflection is about the yaxis, then, the points on the right side of the yaxis gets to the right side of the yaxis, and vice versaIf you change a function like f(x) to f(x), it flips the function over the yaxis!




Inverse Function Reflection In Y Axis Mathematics Stack Exchange
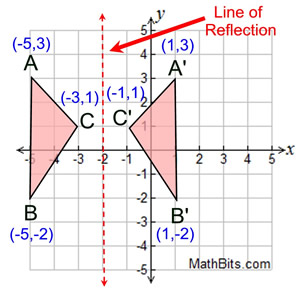



Reflection Mathbitsnotebook A1 Ccss Math
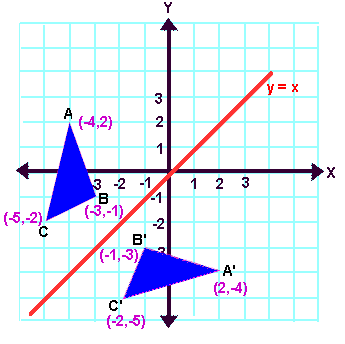
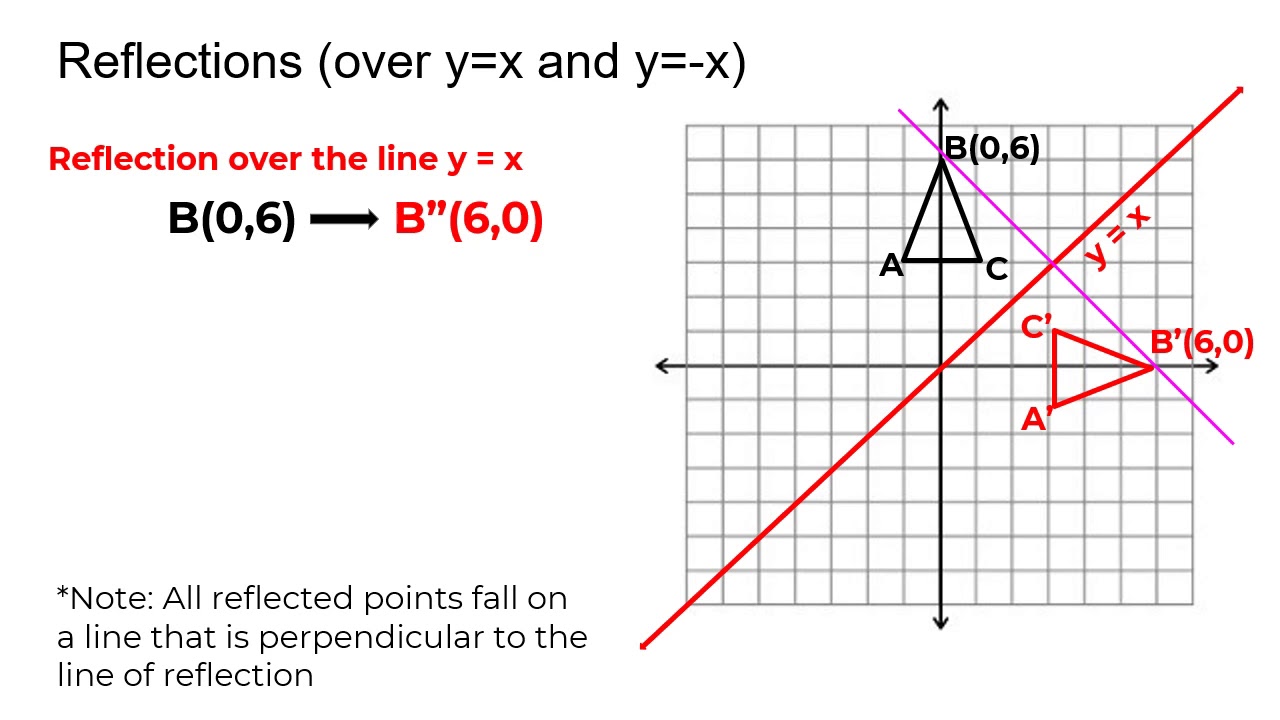
A reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the $$ y = x $$ $ (A,B) \rightarrow (\red B, \red A ) $ When an equation is reflected in the Xaxis the value of #y# is replaced with the negative of that in the original equationAnd also, the line x = 2 (line of reflection) is the perpendicular bisector of the segment joining any point to its image Students can keep this idea in mind when they are working with lines of reflections which are neither the x axis nor the y axis




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
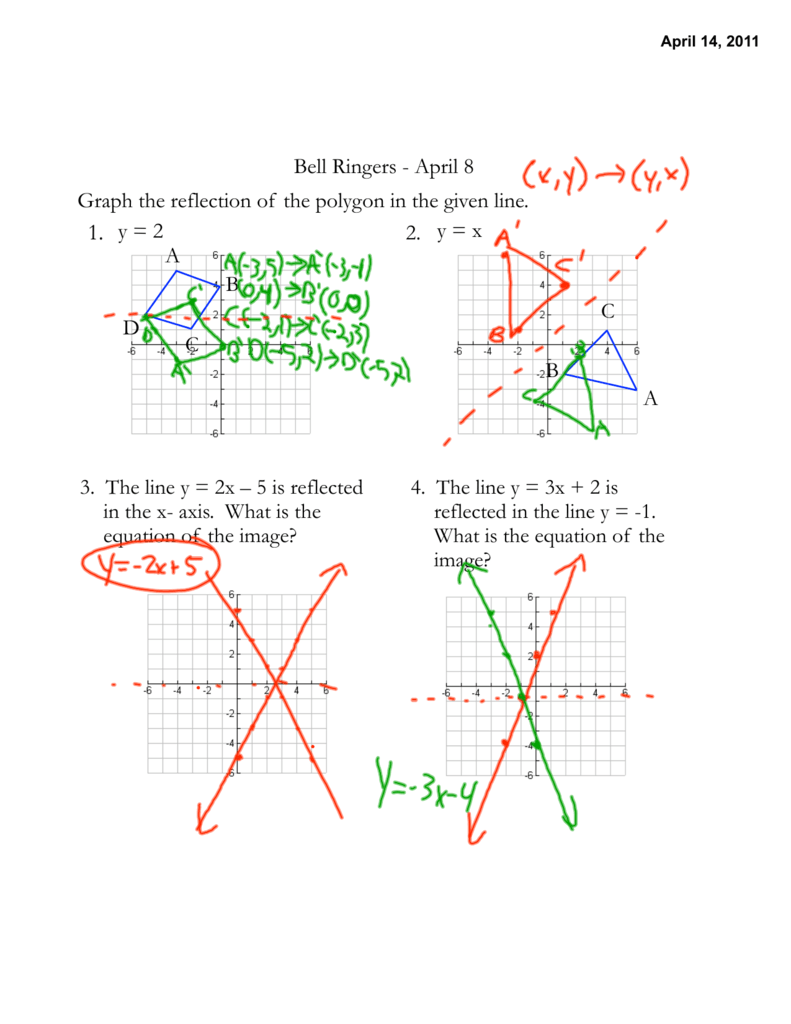



April 8 Graph The Reflection Of The Polygon In The Given Line 1 Y 2
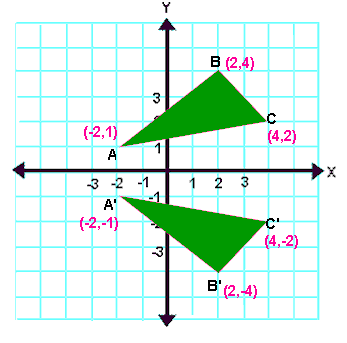
A reflection can be done through yaxis by folding or flipping an object over the y axis The original object is called the preimage, and the reflection is called the image If the preimage is labeled as ABC, then t he image is labeled using a prime symbol, such as A'B'C' An object and its reflection have the same shape and size, but the figures face in opposite directions We are only looking for the transformation that is a reflection over xaxis from parent function Y equals x start superscript 2 end superscript is reflected across the xxxaxis and then scaled vertically by a factor of 43 3 4 start fraction 4 divided by 3 end fraction Picture Of Reflection In The Line Y X Reflection Math Math Types Of ReflectionA reflection of a point over the y axis is shown The rule for a reflection over the y axis is ( x , y ) → ( − x , y ) Reflection in the line y = x
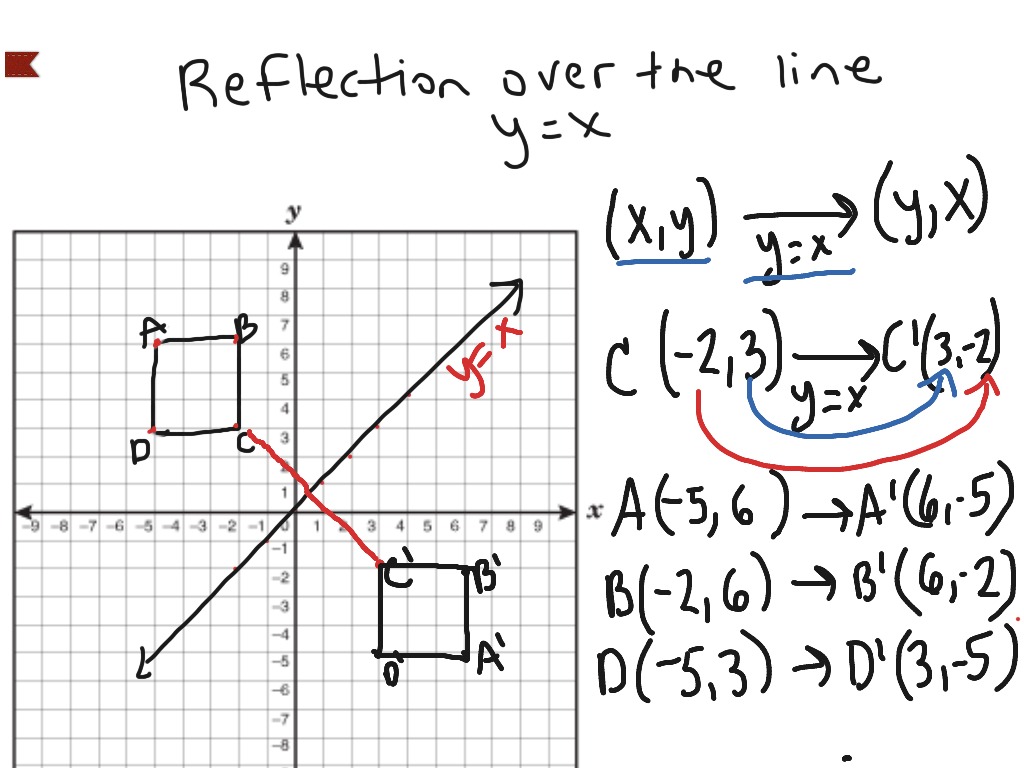



Reflection Over The Line Y X Math Showme



1
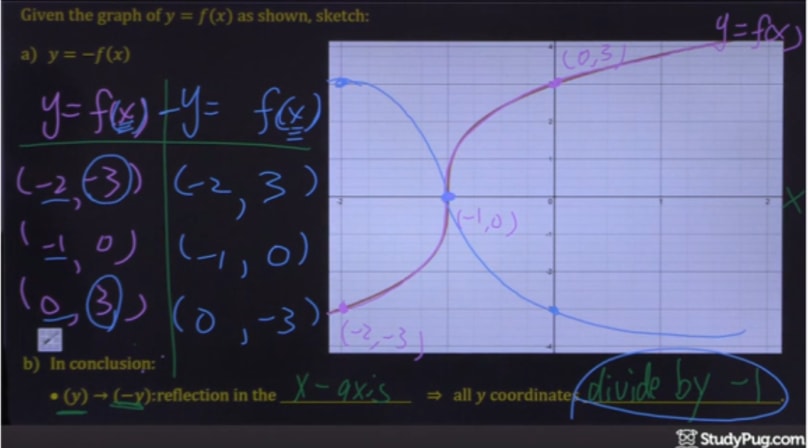
Slide 7 is the most difficult part of this lesson Ask students how to graph y = x They should know how now but still may not remember Graph the line Ask students to start with point A and reflect it over the line My students told me to go left 2 squares to get to y = xx and then 2 more squares past that to create the new lineThe linear transformation rule (p, s) → (r, s) for reflecting a figure over the oblique line y = mx b where r and s are functions of p, q, b, and θ = Tan 1 (m) is shown below Finding the linear transformation rule given the equation of the line of reflection equation y = mx b involves using a calculator to find angle θ = Tan 1 (mThe best way to practice drawing reflections over y axis is to do an example problem Example Given the graph of y = f (x) y=f(x) y = f (x) as shown, sketch y = f (− x) y = f(x) y = f (− x) Remember, the only step we have to do before plotting the f(x) reflection is simply divide the xcoordinates of easytodetermine points on our
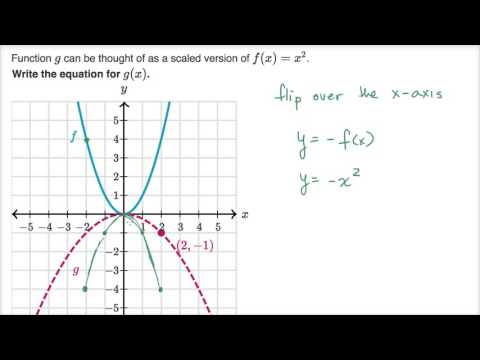



Scaling Reflecting Parabolas Video Khan Academy
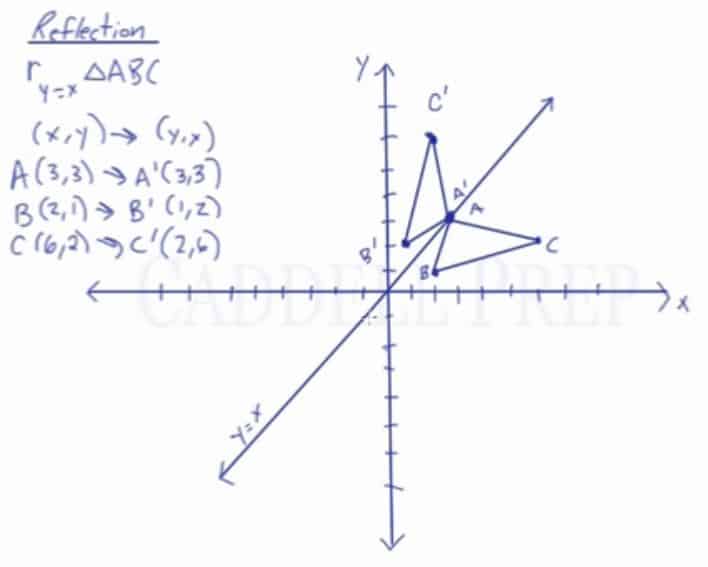



Learn About Reflection Over The Line Y X Caddell Prep Online
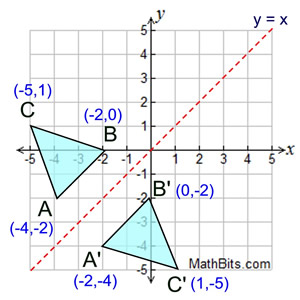



Reflection Mathbitsnotebook A1 Ccss Math
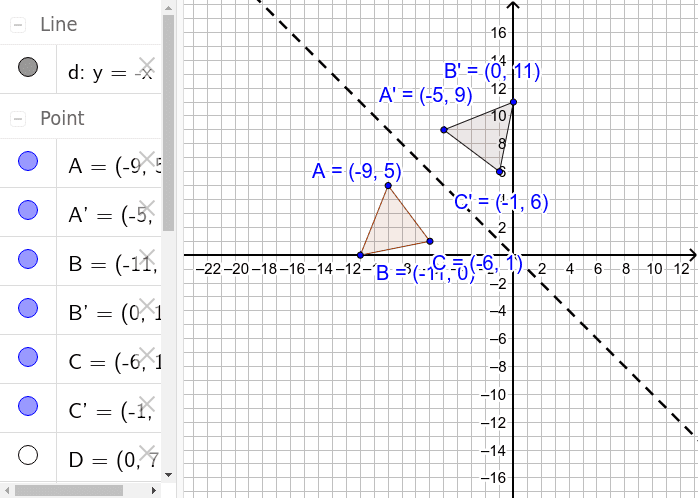



Reflection Over The Line Y X Geogebra



Solution The Line With The Equation Y 2x 3 Is Reflected In The Y Axis Find The Equation Of The Image Line



Reflection Notes Videos Qa And Tests Grade 9 Optional Mathematics Transformation Kullabs




Algebraic Representations Of Reflections
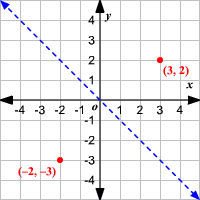



Reflections
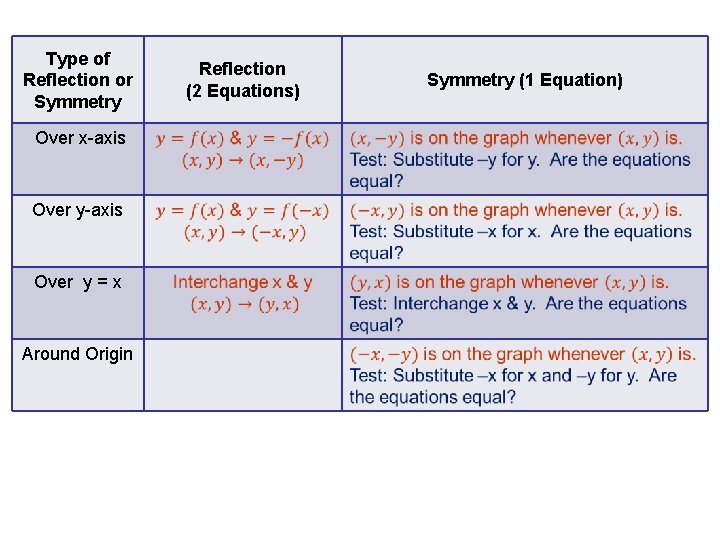



Warm Up Use The Graph To Give The




How To Reflect Quadratic Equations Video Lesson Transcript Study Com
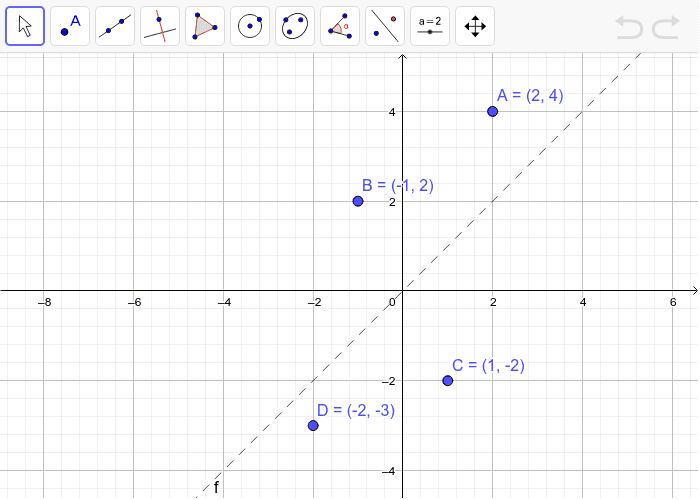



Reflecting In The Line Y X 2 Geogebra
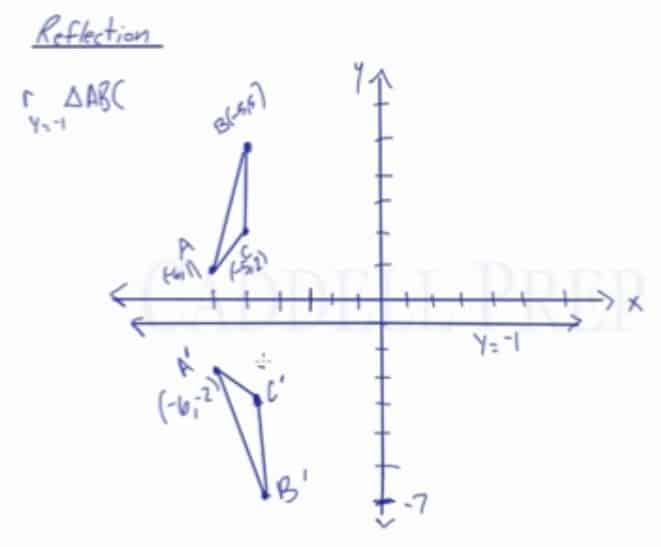



Learn About Reflection Over A Horizontal Or Vertical Line



A Line Segment Goes From 1 2 To 4 1 The Line Segment Is Reflected Across X 1 Reflected Across Y 3 And Then Dilated About 2 2 By A Factor
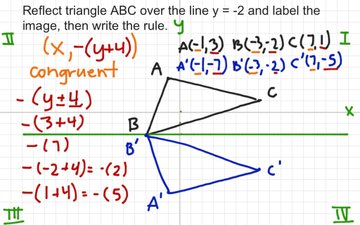



Reflection Over Y 2 With Rule Educreations



How To Prove Say That Point X Y Becomes Y X On A Reflection On The Line Y X Using Only Geometry Quora
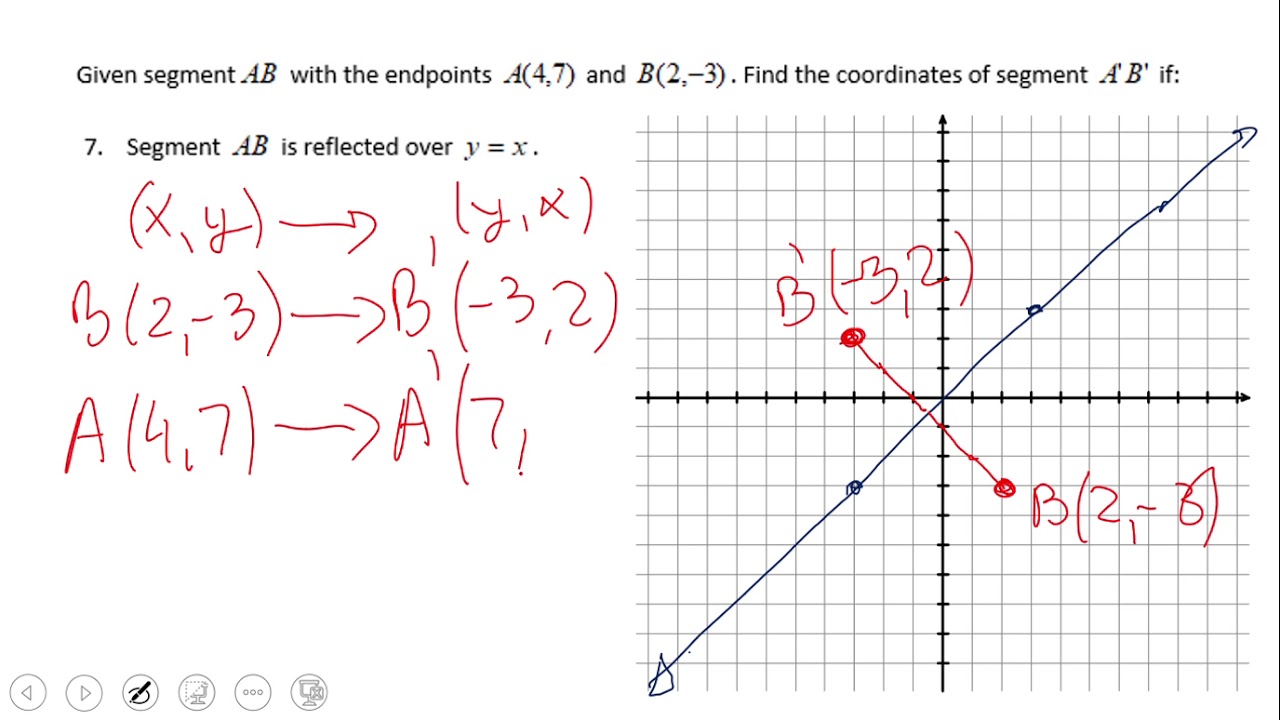



Reflection Over Y X And Y X Youtube



1



Reflect Function About Y Axis F X Expii
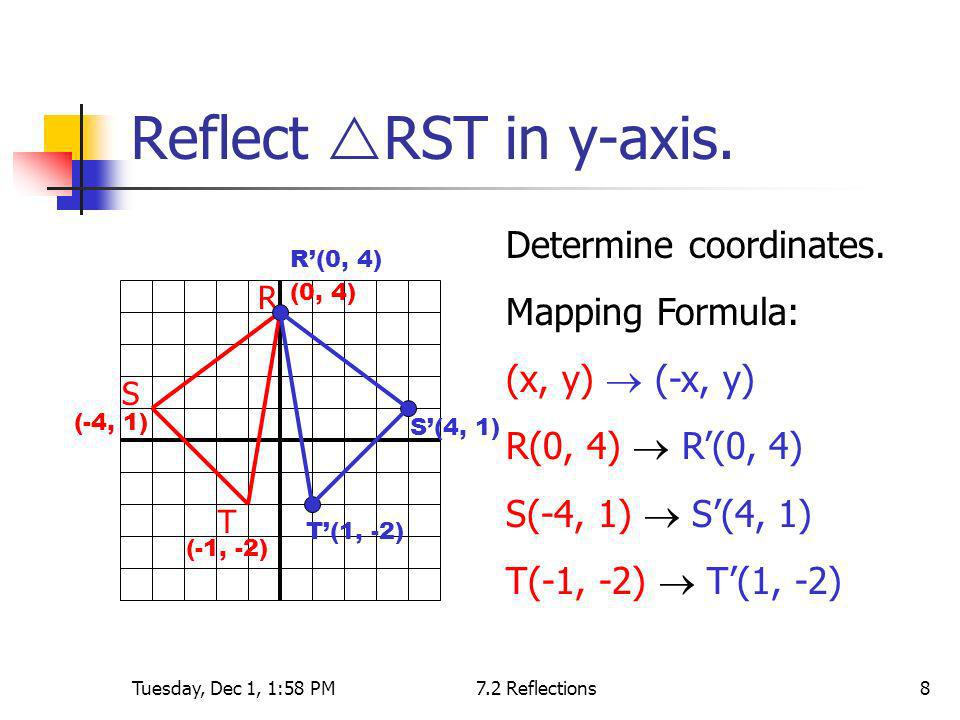



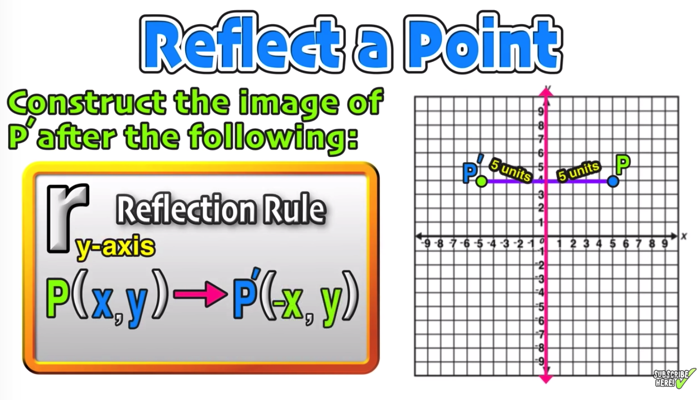
What Are The Coordinates Of Point A 4 1 After It Has Been Reflected Over The Y Axis Socratic




Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor
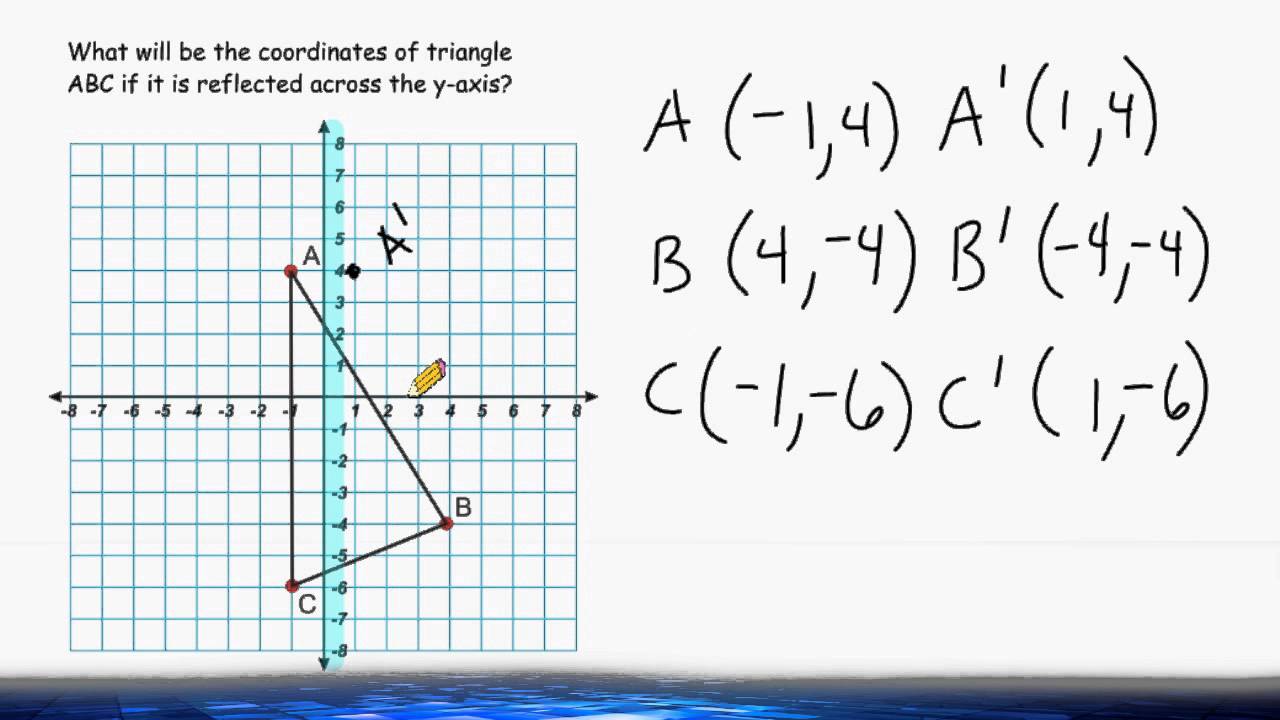



Reflecting A Triangle Across The Y Axis Youtube




Reflection Transformation Matrix



Reflection Transformation



How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics




Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation



Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra



Reflection Over The Y X Line Youtube
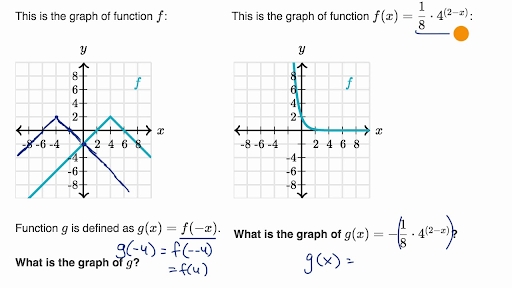



Reflecting Functions Examples Video Khan Academy



Reflection Over The X And Y Axis The Complete Guide Mashup Math




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
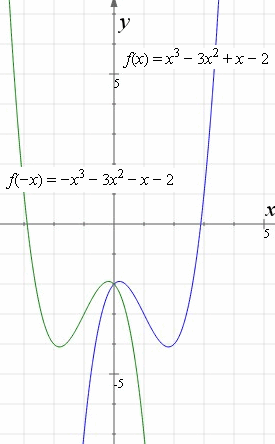



How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics
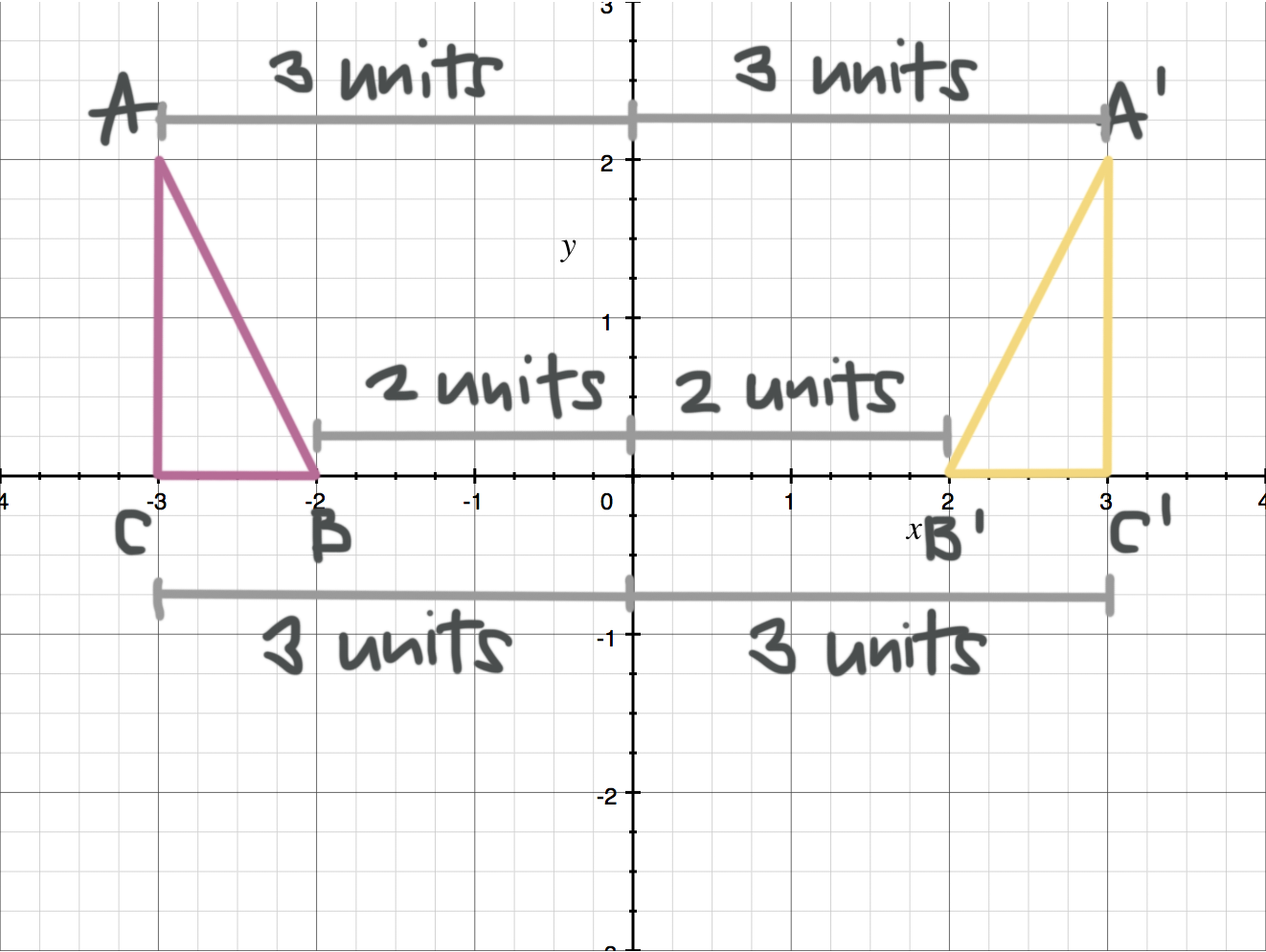



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor




Describing A Reflection Key Stage 2



4 3 Reflecting Graphs Symmetry Learning Objectives Reflect Graphs Use Symmetry To Sketch Graphs Find Lines Of Symmetry How To Use A Line Symmetry Ppt Download
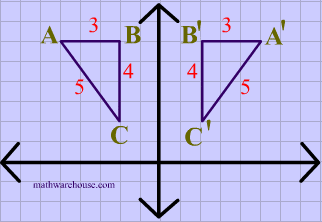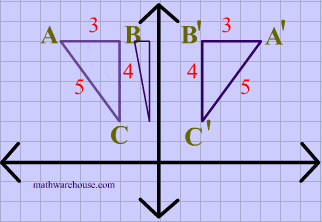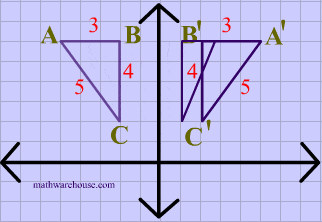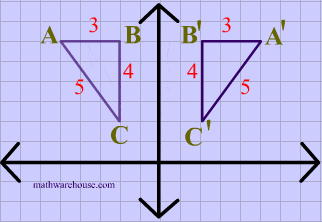



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines



Reflection Mathbitsnotebook A1 Ccss Math
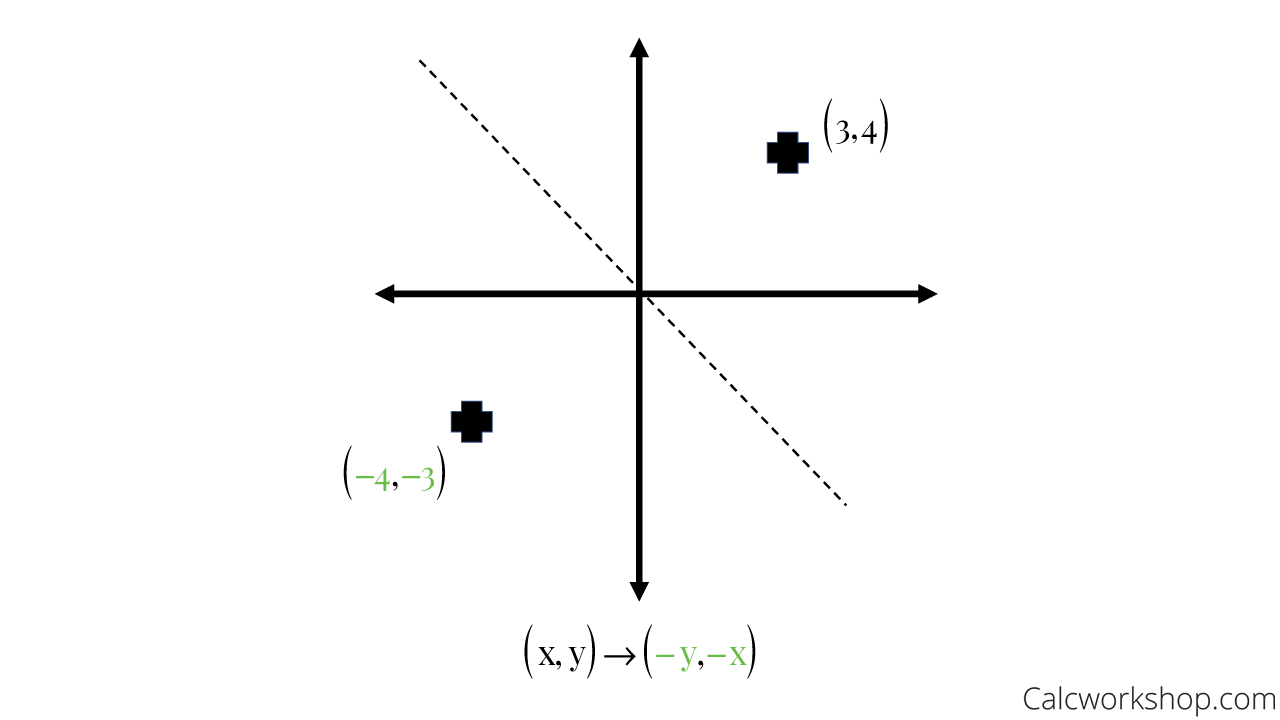



Reflection Rules How To W 25 Step By Step Examples



Reflection Over The X And Y Axis The Complete Guide Mashup Math
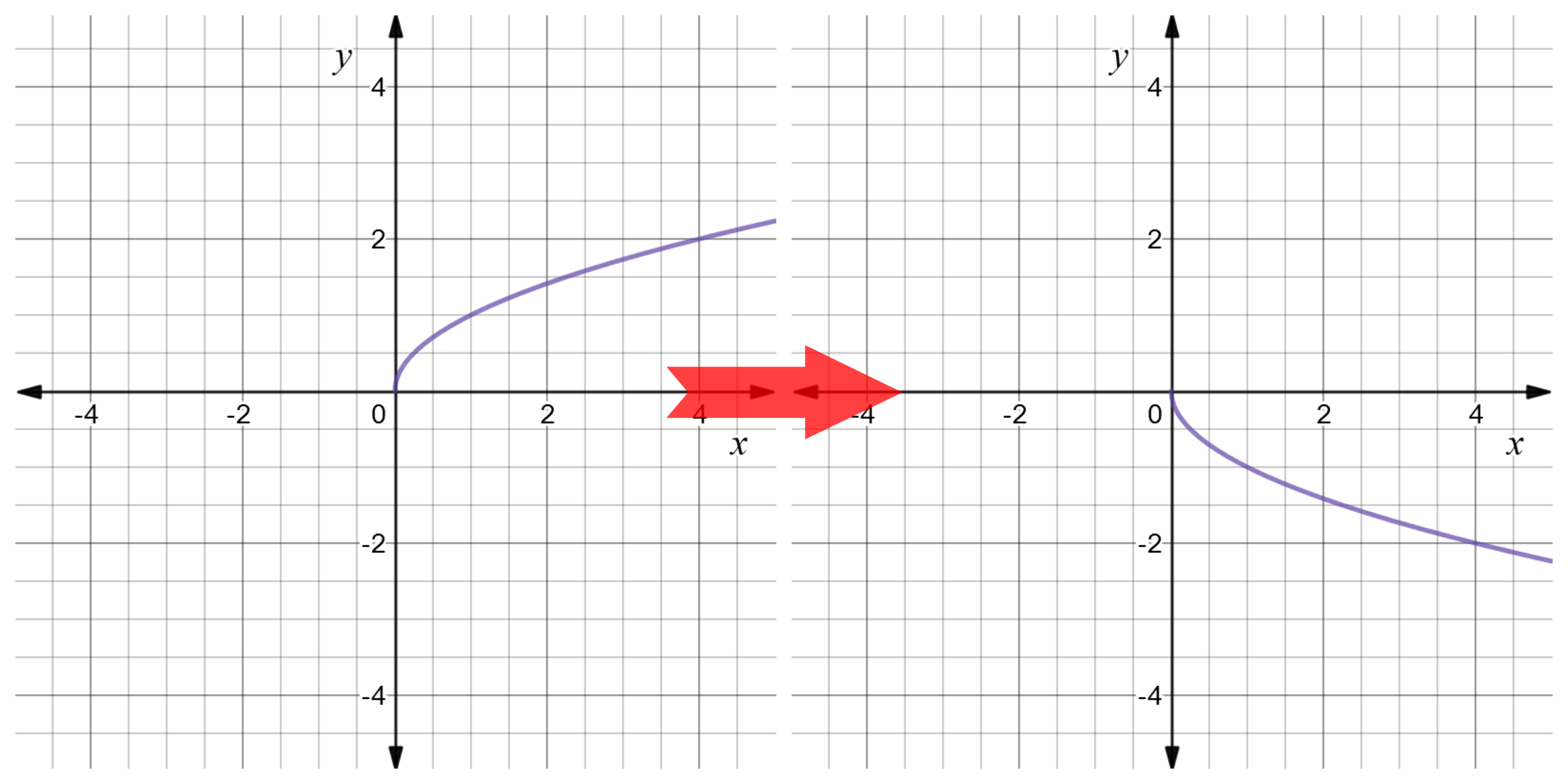



Reflect Function About Y Axis F X Expii
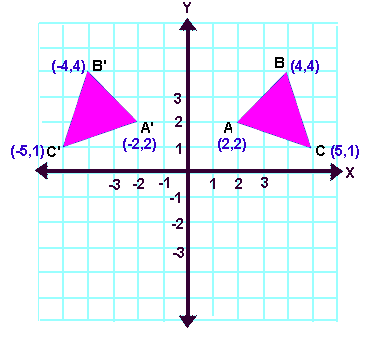



Reflection Transformation




Solved The Graph Shown To The Right Involves A Reflection In Chegg Com




The Equation Of A Line Reflected About Another Line Mathematics Stack Exchange




Reflections Ck 12 Foundation



Assignment 2 Transforming Parabolas
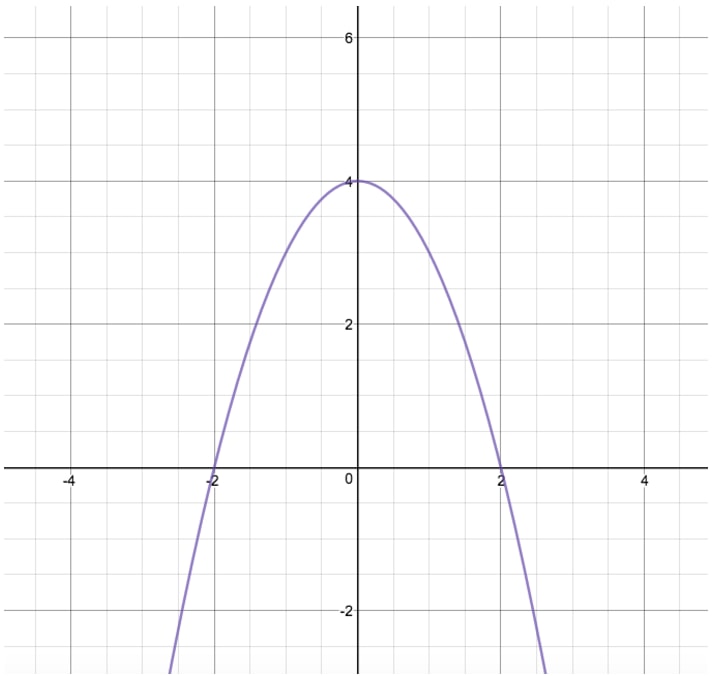



How To Reflect A Graph Through The X Axis Studypug
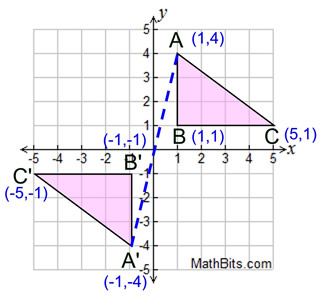



Reflection Mathbitsnotebook A1 Ccss Math




Picture Of Reflection In The Line Y X Reflection Math Common Myths Types Of Reflection



Assignment 2 Transforming Parabolas



Reflection Rules How To W 25 Step By Step Examples



What Does It Mean To Reflect Over The Y X Line Quora




Picture Of Reflection Across Y Axis Reflection Math Math Reflection



Scaling Reflecting Parabolas Video Khan Academy



Reflection Over The X And Y Axis The Complete Guide Mashup Math



Reflection Transformation
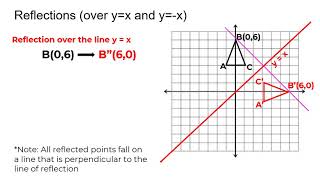



Reflection Over The Y X Line Youtube
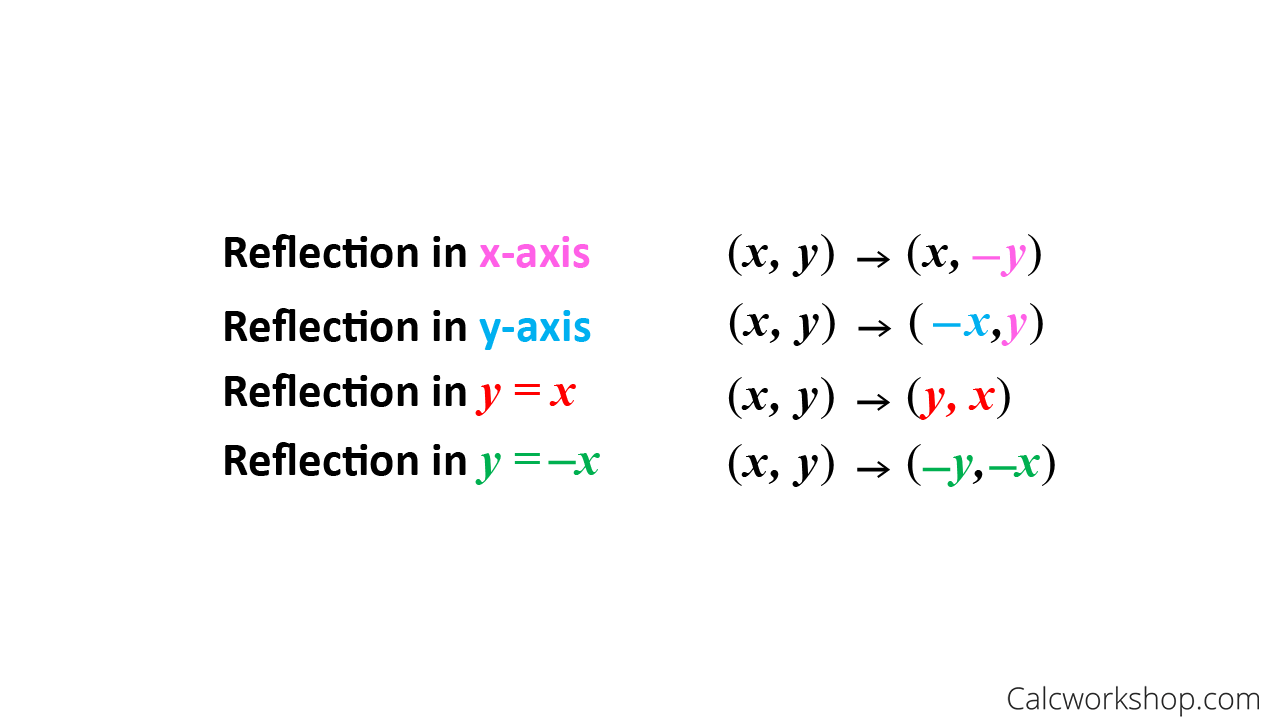



Reflection Rules How To W 25 Step By Step Examples




Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation



Solution After A Reflection In The Line Y X 8 3 Is The Image Of Point Q What Is The Original Location Of Point Q
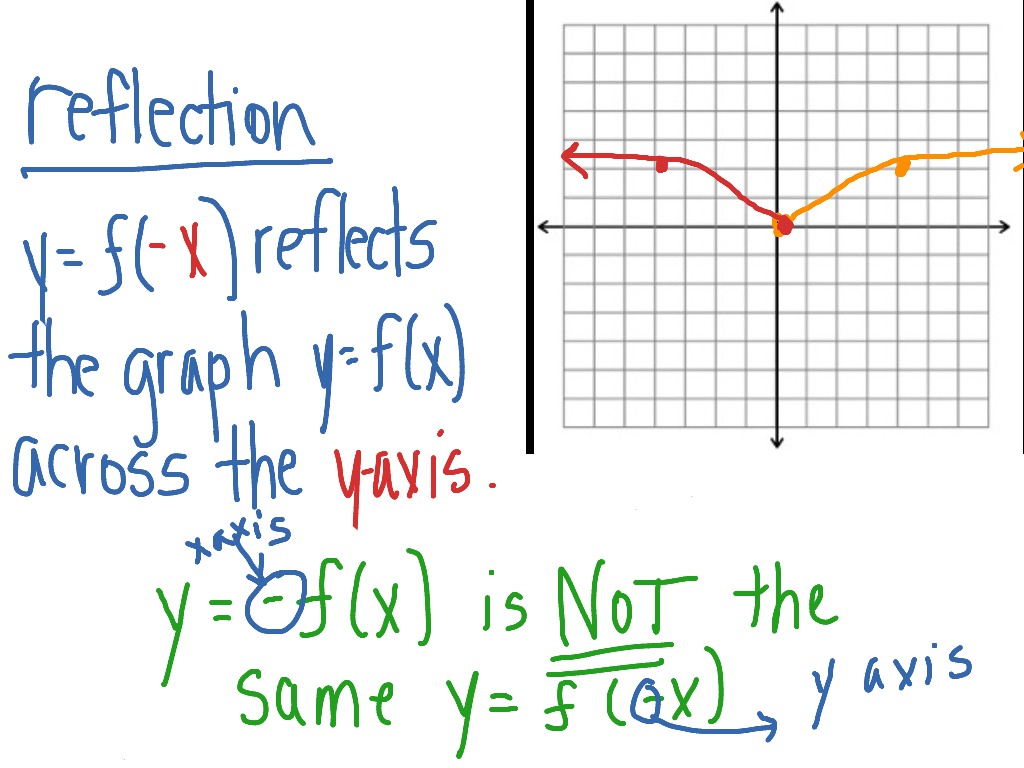



Reflection Across The Y Axis Math Functions Showme



Assignment 2 Transforming Parabolas



Solution After A Reflection In The Line Y X 2 4 Is The Image Of Point N What Is The Original Location Of Point N
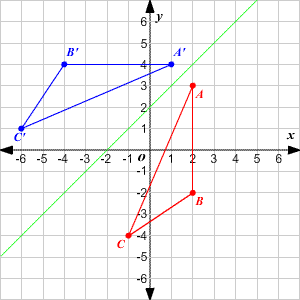



Transformations Of Graphs
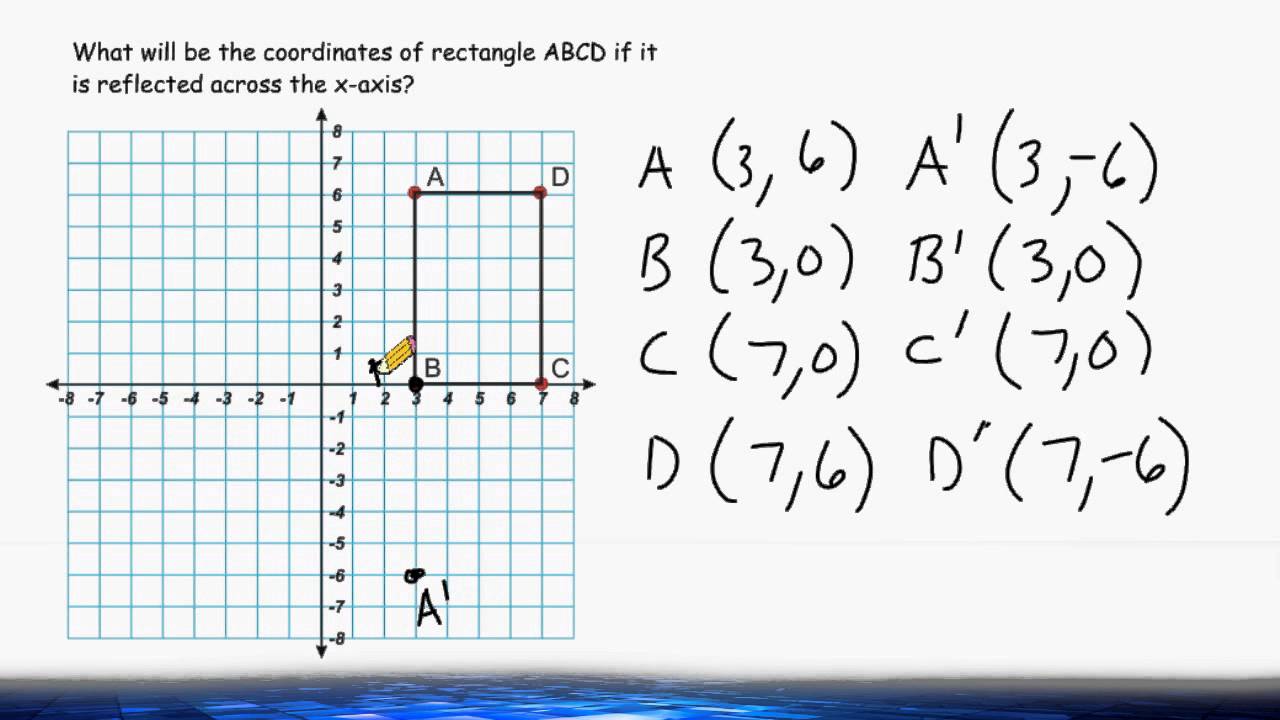



Transformations Reflection Across The X Axis Youtube
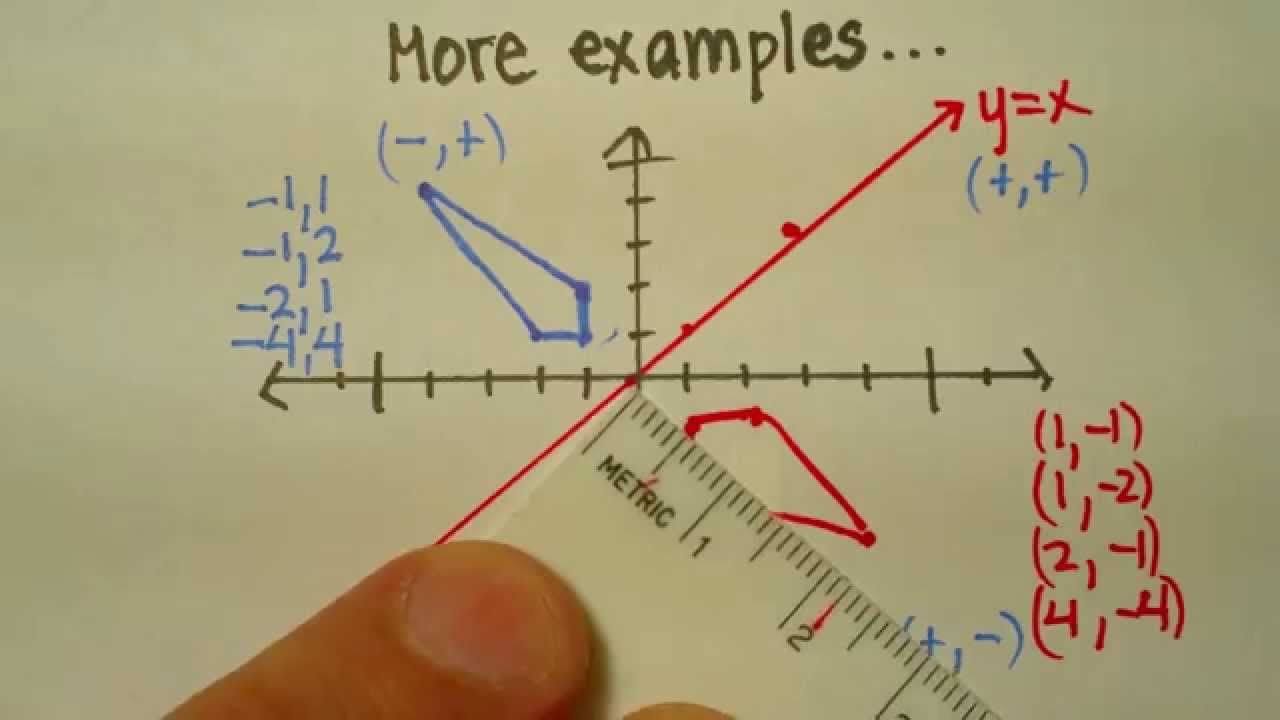



Transformation Reflection Across Y X Youtube



A Review Of Logarithms



Math Alive Geometry 1
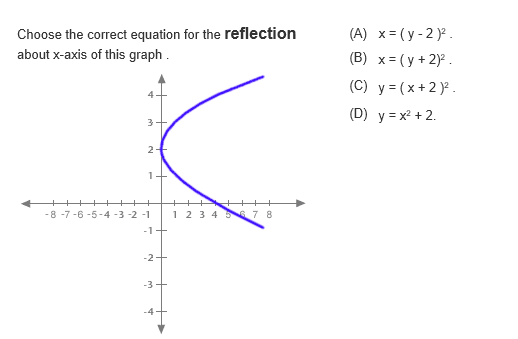



Solved Choose The Correct Equation For The Reflection About Chegg Com




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3
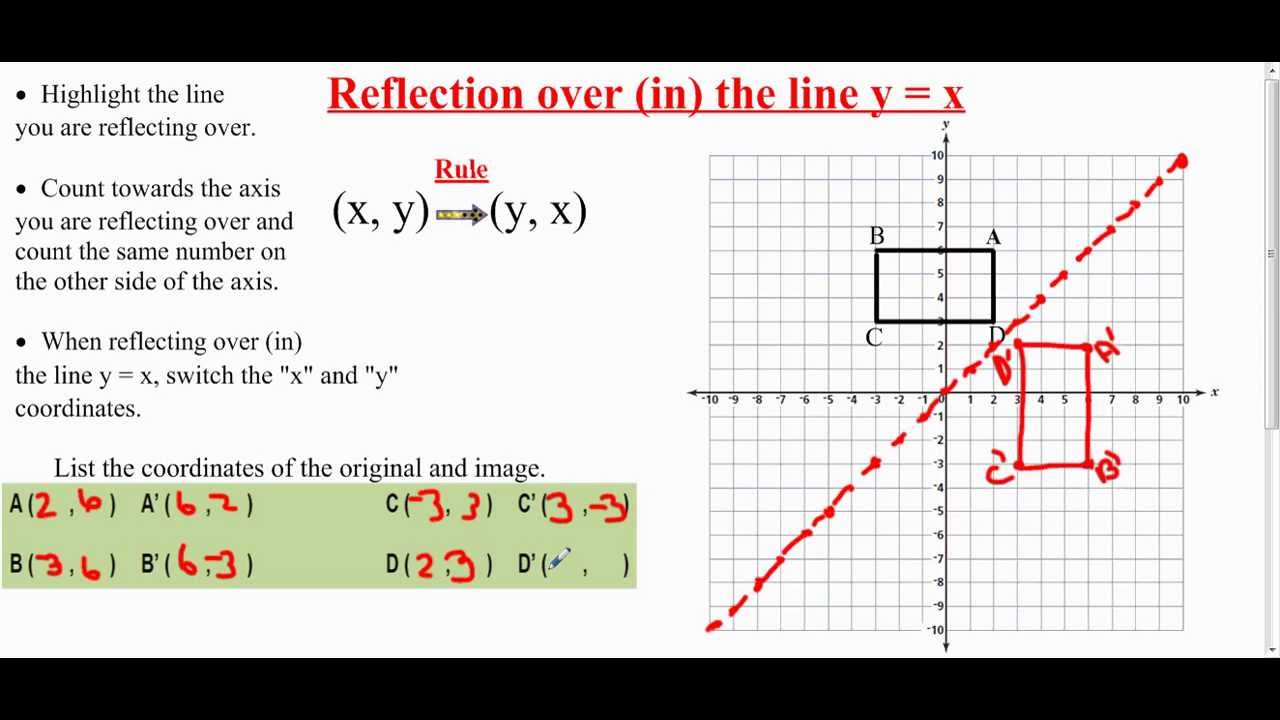



Transformation Reflection Over The Line Y X Youtube
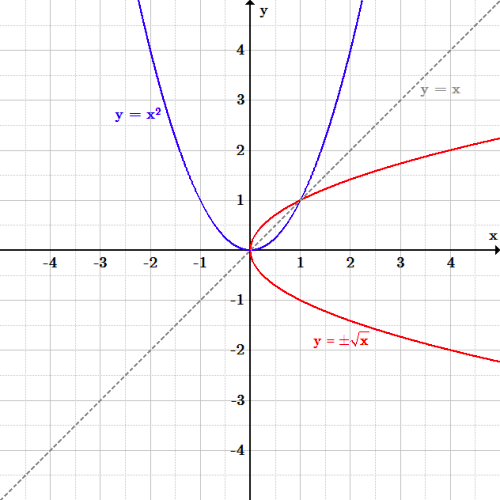



Transformations Boundless Algebra
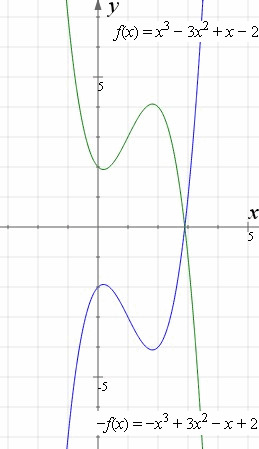



How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics




Reflecting Shapes Article Reflections Khan Academy




Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation
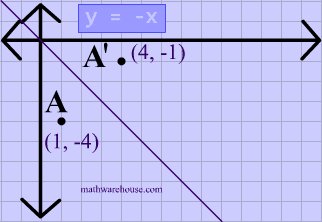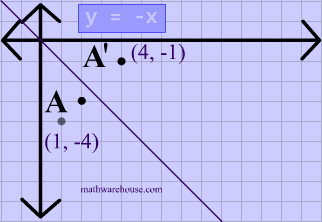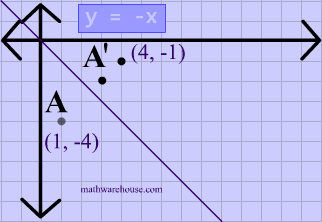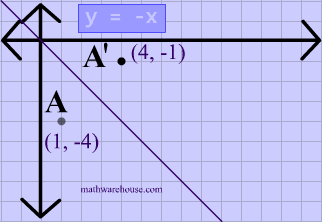



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com



Reflection Objectives D Gradereflect Shapes In Lines Such As X 2 Or Y 1 Describe Reflections Fully Identify Reflection Symmetry In 3 D Solids Prior Ppt Download



Ch 3 4
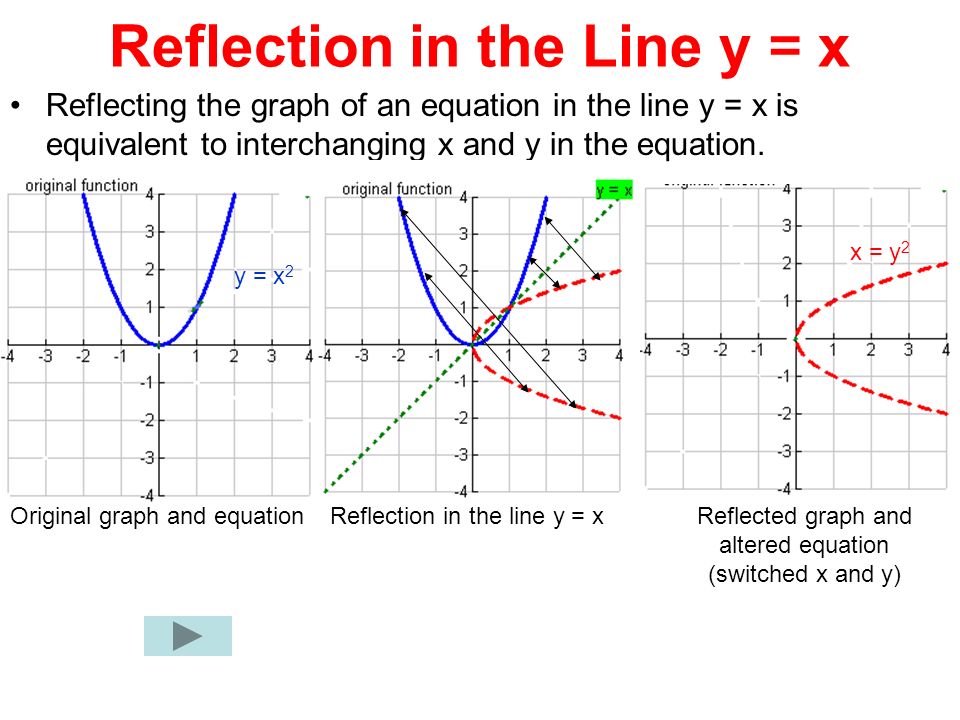



Section 4 3 Reflecting Graphs Symmetry Objective To Reflect Graphs And To Use Symmetry To Sketch Graphs Ppt Download
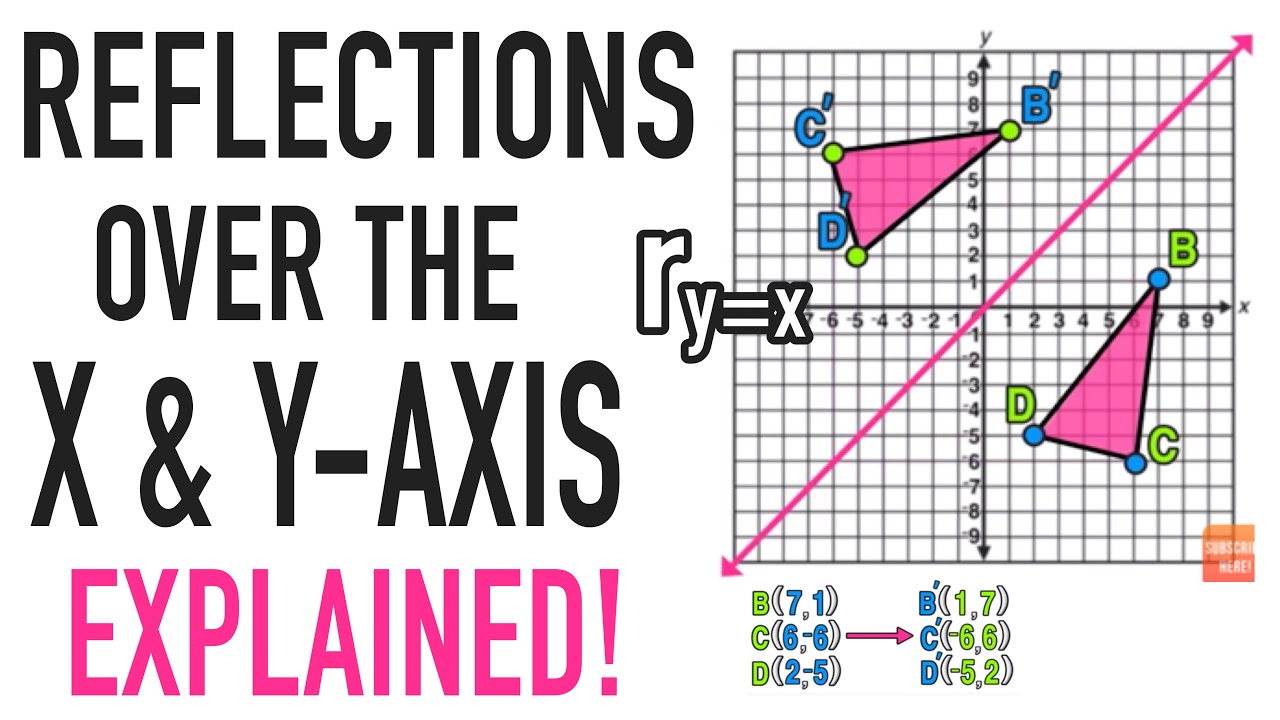



Reflections Over The X Axis And Y Axis Explained Youtube




Reflection Over Y X Math Geometry Showme



0 件のコメント:
コメントを投稿